一直覺得 Attention is all you need 也就是提出 Transformer 的那篇 paper，裡面提到 positional encoding 的想法很有趣。
剛好在 HW5 的 report 中，有一個題目是關於 position embedding 的探索如下：

Given a (N x D) positional embeding lookup table, you aim to get a (N x N) “similarity matrix” by calculating similarity between different pairs of embeddings in the table. You need to visualize the similarity matrix and briefly explain the result. In this problem, we focus on the positional embeddings of the decoder .

於是我用下列這段 code 取出 decoder 的 positional embedding:

pos_emb = model.decoder.embed_positions.weights.cpu().detach()

並將之可視化如下: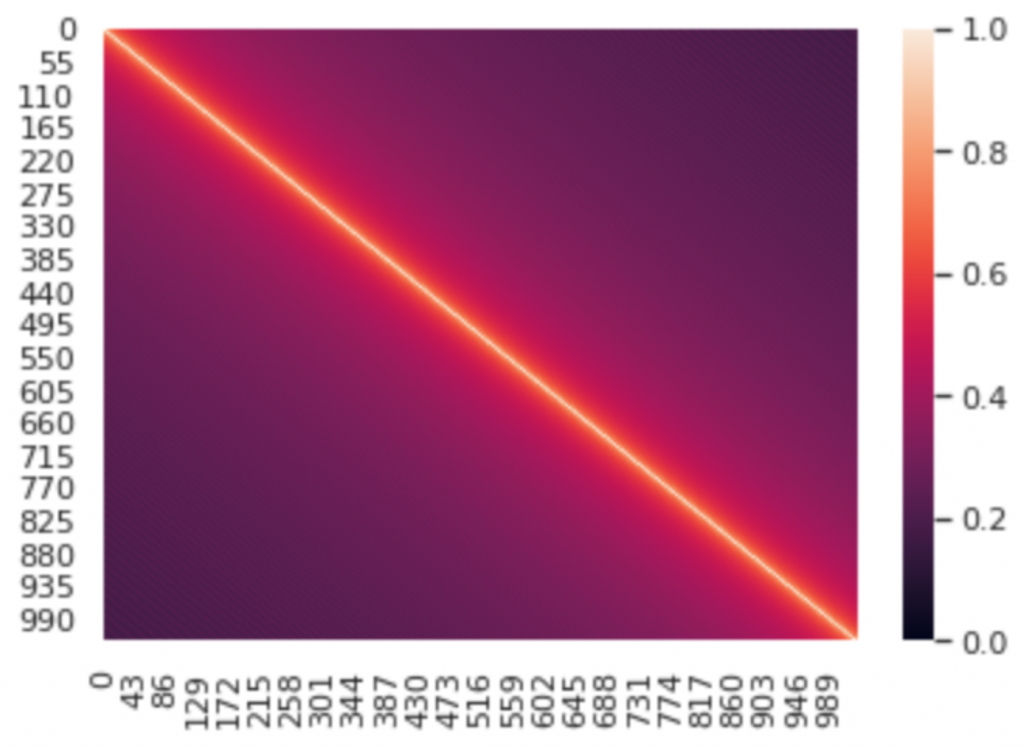

可以發現在計算 1026 個 position embedding 之間的 cosine similarity 之後，和自己的位 置的embedding 的相似度是最高的(diagonal 上的值都是1)，而距離自己位置越遠的 positional embedding 的相似度就越低，所以呈現從 diagonal 向兩旁遞減的趨勢。

這是因為 Transformer 採用 sinusoidal function 來 encode positional information 如下:

所以每個 position embedding 會長的像下面這個矩陣: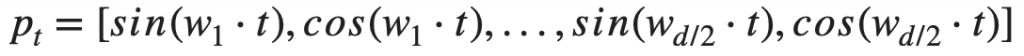

他們使用這個 function 可以讓 model 很容易地學會 token 之間的 relative positional information，因為任意的 pt+φ 和 pt 之間可以用一個 linear function 來轉換: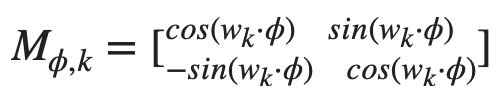

因此這邊如果我們把問題簡化，positional embedding size 設為 2，那下一個字的 positional embedding 就相當於把前一個字的 embedding 做逆時針旋轉，因此距離越遠的字，embedding 的夾角越大， cosine similarity 自然也就會越低了。